这是一个非常常见且重要的问题,Java 中的 double 类型不保证有固定的小数位数,它是一个近似值,而不是精确值。
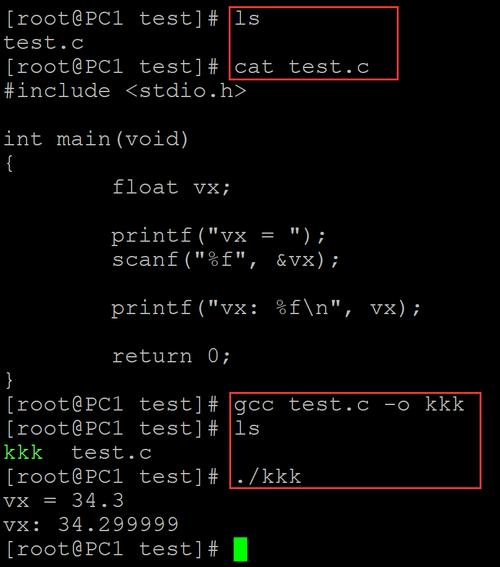
下面我将从几个方面详细解释这个问题:
核心原因:二进制浮点数
计算机的底层是基于二进制的。double 类型遵循 IEEE 754 标准,使用二进制科学记数法来表示小数。
关键问题:很多十进制小数无法在二进制中精确表示。
-
十进制可以精确表示的例子:
 (图片来源网络,侵删)
(图片来源网络,侵删)5(二进制:1)25(二进制:01)125(二进制:001)- 这些都是
2的负整数次方,所以可以精确转换。
-
十进制无法精确表示的例子(最经典的 0.1):
- 十进制的
1在二进制中是一个无限循环小数:00011001100110011... - 由于
double的存储位数是有限的(64位),它只能存储这个无限循环小数的一个近似值。 - 你在代码中写的
1,在计算机内部存储的并不是精确的1,而是一个非常接近它的数。
- 十进制的
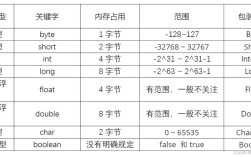
double 的精度和范围
一个 double 占用 64 位(8字节),其结构如下:
- 1 位:符号位(正或负)
- 11 位:指数部分(决定数值的大小范围)
- 52 位:尾数部分(决定数值的精度)
精度:
- 尾数有 52 位,加上隐藏的 1 位,总共是 53 位的二进制精度。
- 这大约相当于 15 到 17 位十进制有效数字。
- 注意:这是指“有效数字”的总位数,而不是“小数点后的位数”。
67有 15 位有效数字,00000000000000123也有 15 位有效数字。
范围:
- 指数部分决定了
double的表示范围,大约是-1.7 x 10⁸⁰⁸到7 x 10³⁰⁸。
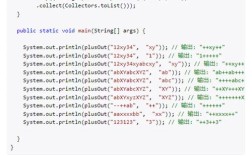
代码示例:直观感受 double 的不精确性
public class DoublePrecision {
public static void main(String[] args) {
// 1. 经典例子:0.1
double d1 = 0.1;
System.out.println("直接打印 0.1: " + d1); // 输出可能是 0.1,但这是 println() 的“美化”结果
System.out.println("使用 printf 显示更多小数位: %.20f%n", d1); // 输出: 0.10000000000000000555
// 2. 简单的算术运算
double d2 = 0.1 + 0.2;
System.out.println("0.1 + 0.2 = " + d2); // 输出: 0.30000000000000004
System.out.println("0.1 + 0.2 == 0.3? " + (d2 == 0.3)); // 输出: false
// 3. 有效数字的例子
double bigNumber = 123456789012345.67;
System.out.printf("大数 %.15f%n", bigNumber); // 精度足够,能正确显示
System.out.printf("大数 %.20f%n", bigNumber); // 超出精度,后面的数字就不准了
double smallNumber = 0.12345678901234567;
System.out.printf("小数 %.20f%n", smallNumber); // 精度足够
}
}
运行结果分析:
1的实际存储值略大于1。1 + 0.2的结果因为两个近似值的相加,误差被放大,导致结果变成了30000000000000004,而不是3,这使得简单的 比较变得不可靠。
如何正确处理 double 的小数位?
既然 double 不精确,我们在需要精确表示或显示小数位时,应该怎么做?
用于显示(格式化输出)
如果你只是想把 double 的值显示成固定的小数位(2 位,代表货币),可以使用 String.format() 或 System.out.printf()。
double price = 99.995;
// 四舍五入并格式化为两位小数
String formattedPrice = String.format("%.2f", price); // "100.00"
System.out.println(formattedPrice);
// 使用 printf
System.out.printf("价格是: %.2f 元%n", price); // 价格是: 100.00 元
注意:这只是格式化显示,price 变量本身的值并没有改变,它依然是一个不精确的 double 值。
用于精确计算(金融、财务等)
如果你需要进行精确的数学运算,特别是涉及金钱的场景,绝对不要使用 double,你应该使用 java.math.BigDecimal 类。
BigDecimal 可以表示任意精度的十进制数,它解决了 double 的不精确问题。
import java.math.BigDecimal;
import java.math.RoundingMode;
public class BigDecimalExample {
public static void main(String[] args) {
// 使用字符串构造 BigDecimal,避免 double 的不精确问题
BigDecimal bd1 = new BigDecimal("0.1");
BigDecimal bd2 = new BigDecimal("0.2");
// 进行精确的加法
BigDecimal sum = bd1.add(bd2);
System.out.println("0.1 + 0.2 (使用 BigDecimal) = " + sum); // 输出: 0.3
System.out.println("0.1 + 0.2 == 0.3? " + sum.equals(new BigDecimal("0.3"))); // 输出: true
// 设置小数位数和舍入模式
BigDecimal price = new BigDecimal("99.995");
BigDecimal roundedPrice = price.setScale(2, RoundingMode.HALF_UP); // 四舍五入,保留两位小数
System.out.println("四舍五入后的价格: " + roundedPrice); // 输出: 100.00
}
}
| 问题/场景 | double |
BigDecimal |
|---|---|---|
| 本质 | 二进制浮点数,近似值 | 十进制数字,精确值 |
| 精度 | 约 15-17 位有效数字 | 任意精度(受内存限制) |
| 用途 | 科学计算、图形学、物理模拟等对性能要求高、对绝对精度要求不高的场景 | 金融、财务、电商等需要精确计算的场景 |
| 显示 | 需用 printf 或 String.format 格式化 |
可直接 toString(),或用 setScale() 控制小数位 |
| 性能 | 快,直接由 CPU 支持 | 慢,基于软件实现,涉及对象创建 |
核心结论:
double有多少位小数? 没有固定答案,它的精度是有限的(约15-17位有效数字),且是二进制的,很多十进制小数无法精确表示。- 为什么
1 + 0.2 != 0.3? 因为1和2在计算机中都是近似值,它们的相加结果也是一个近似值,恰好不等于3的近似值。 - 什么时候用
double? 用于非精确的科学计算。 - 什么时候用
BigDecimal? 用于需要精确表示和计算的场景,特别是货币。