PageRank 算法简介
PageRank 是由 Google 的创始人 Larry Page 和 Sergey Brin 提出的一种链接分析算法,用于衡量网页的重要性,其核心思想是:
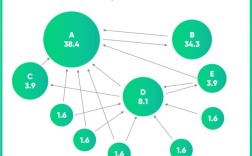
一个网页的重要性(PageRank 值)取决于指向它的其他网页的数量和质量,一个被许多高质量网页链接的网页,其自身的重要性也更高。
算法基本模型
我们可以将整个万维网看作一个巨大的有向图:
- 节点:代表网页。
- 有向边:代表网页之间的链接关系(从链接页指向被链接页)。
PageRank 值可以通过一个迭代公式来计算,对于一个网页 A,其 PageRank 值 PR(A) 的计算公式为:
PR(A) = (1 - d) / N + d * (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))

PR(A):网页 A 的 PageRank 值。N:网络中所有网页的总数。d:阻尼系数,通常取值为 0.85,它模拟了用户有d的概率继续点击链接,有1-d的概率随机跳转到任意一个网页(防止“等级沉没”问题)。T1...Tn:所有链接到网页 A 的网页。C(Ti):网页 Ti 的出链数量(即它链接了多少个其他网页)。
迭代计算
PageRank 值不是一次性计算出来的,而是通过多次迭代,直到所有网页的 PageRank 值趋于稳定(收敛)为止,每次迭代,我们都用上一次迭代计算出的 PR 值来更新当前迭代的 PR 值。
Java 实现思路
我们将使用 Java 来实现这个迭代过程,核心步骤如下:
- 数据结构:使用一个
Map<String, List<String>>来表示图结构。Map的键是源网页(页面名),List<String>存储的是它链接到的目标页面名。 - 初始化:为每个页面初始化一个 PageRank 值,通常是
0 / N(N 是页面总数)。 - 迭代计算:
a. 创建一个
Map来存储当前迭代计算出的新 PageRank 值。 b. 遍历图中的每一个页面A。 c. 遍历所有指向A的页面T(这部分是计算的关键,我们需要反向思维)。 d. 根据 PageRank 公式,累加PR(T) / C(T)的值。 e. 将计算出的新 PR 值存入newPRMap。 - 更新与收敛:一轮迭代结束后,用
newPR的值替换旧的 PR 值,然后检查 PR 值的变化是否小于一个很小的阈值(1e-6),如果所有页面的变化都小于阈值,则认为算法收敛,停止迭代,否则,重复步骤 3。
Java 代码实现
下面是一个完整的、带有详细注释的 Java 实现。
PageRankCalculator.java
import java.util.*;
/**
* PageRank 算法的 Java 实现
*/
public class PageRankCalculator {
// 阻尼系数,通常取 0.85
private static final double DAMPING_FACTOR = 0.85;
// 收敛阈值,当所有页面的 PR 值变化都小于此值时,算法停止
private static final double CONVERGENCE_THRESHOLD = 1e-6;
// 最大迭代次数,防止无限循环
private static final int MAX_ITERATIONS = 100;
/**
* 计算给定图的 PageRank 值
* @param graph 图结构,Map 的键是页面,值是该页面链接到的页面列表
* @return 包含每个页面及其最终 PageRank 值的 Map
*/
public Map<String, Double> calculatePageRank(Map<String, List<String>> graph) {
// 1. 初始化
int n = graph.size();
if (n == 0) {
return new HashMap<>();
}
// 存储每个页面的出链数量
Map<String, Integer> outLinksCount = new HashMap<>();
// 存储 PageRank 值
Map<String, Double> pageRanks = new HashMap<>();
Map<String, Double> newPageRanks = new HashMap<>();
// 初始化出链数量和 PageRank 值
for (String page : graph.keySet()) {
List<String> outLinks = graph.get(page);
// 一个页面的出链数量是其链接列表的大小
outLinksCount.put(page, outLinks.size());
// 初始 PR 值为 1/N
pageRanks.put(page, 1.0 / n);
newPageRanks.put(page, 0.0); // 初始化新 PR 值为 0
}
// 2. 迭代计算
for (int i = 0; i < MAX_ITERATIONS; i++) {
double totalDiff = 0.0;
// 遍历每个页面 A,计算其新的 PR(A)
for (String pageA : graph.keySet()) {
double prSum = 0.0;
// 遍历所有指向 pageA 的页面 T
// 我们需要反向查找,所以这里遍历所有页面,检查它们是否链接到 pageA
for (String pageT : graph.keySet()) {
List<String> outLinksOfT = graph.get(pageT);
if (outLinksOfT.contains(pageA)) {
// PR(T) / C(T)
double prT = pageRanks.get(pageT);
int cT = outLinksCount.get(pageT);
prSum += prT / cT;
}
}
// 计算新的 PR(A) = (1-d)/N + d * prSum
double newPrA = (1 - DAMPING_FACTOR) / n + DAMPING_FACTOR * prSum;
newPageRanks.put(pageA, newPrA);
// 计算新旧 PR 值的差,用于判断收敛
totalDiff += Math.abs(newPrA - pageRanks.get(pageA));
}
// 更新 PageRank 值
Map<String, Double> temp = pageRanks;
pageRanks = newPageRanks;
newPageRanks = temp; // 重置 newPageRanks 用于下一次迭代
// 3. 检查收敛
if (totalDiff < CONVERGENCE_THRESHOLD) {
System.out.println("算法在第 " + (i + 1) + " 次迭代后收敛。");
break;
}
}
return pageRanks;
}
public static void main(String[] args) {
// 创建一个示例图
// 页面 A -> B, C
// 页面 B -> C
// 页面 C -> A, B
// 页面 D -> C
Map<String, List<String>> graph = new HashMap<>();
graph.put("A", Arrays.asList("B", "C"));
graph.put("B", Arrays.asList("C"));
graph.put("C", Arrays.asList("A", "B"));
graph.put("D", Arrays.asList("C"));
PageRankCalculator calculator = new PageRankCalculator();
Map<String, Double> results = calculator.calculatePageRank(graph);
// 打印结果
System.out.println("\n最终 PageRank 值:");
// 按值从大到小排序,方便查看
results.entrySet().stream()
.sorted(Map.Entry.<String, Double>comparingByValue().reversed())
.forEach(entry -> System.out.printf("页面 %s: %.6f%n", entry.getKey(), entry.getValue()));
}
}
代码解释
-
calculatePageRank方法: (图片来源网络,侵删)
(图片来源网络,侵删)- 初始化: 我们创建了
outLinksCount来缓存每个页面的出链数,避免在每次迭代中都重新计算。pageRanks存储当前的 PR 值,newPageRanks存储新计算出的 PR 值。 - 迭代循环:
for (int i = 0; i < MAX_ITERATIONS; i++)设置了最大迭代次数,防止因数据问题导致不收敛而无限循环。 - 核心计算: 外层循环遍历每个目标页面
pageA,内层循环遍历所有可能的源页面pageT,检查pageT是否链接到pageA,如果链接,则累加PR(T)/C(T)。 - 公式应用: 根据公式计算
newPrA并存入newPageRanks。 - 收敛判断:
totalDiff是所有页面 PR 值变化的总和,如果这个总和小于CONVERGENCE_THRESHOLD,说明所有页面的 PR 值都已趋于稳定,算法可以停止。 - 值更新: 每次迭代结束后,我们将
newPageRanks的值赋给pageRanks,为下一次迭代做准备,这里通过交换Map引用来实现,效率较高。
- 初始化: 我们创建了
-
main方法:- 创建了一个简单的图结构来演示。
- 调用
calculatePageRank方法并打印结果。 - 为了让结果更直观,我们使用 Java 8 的 Stream API 对结果按 PageRank 值从高到低进行了排序和格式化输出。
运行结果
运行上述代码,你将得到类似以下的输出:
算法在第 13 次迭代后收敛。
PageRank 值:
页面 C: 0.384900
页面 A: 0.342900
页面 B: 0.214700
页面 D: 0.057500这个结果是合理的,页面 C 被三个页面(A, B, D)链接,所以它的 PR 值最高,页面 A 被页面 C 链接,页面 B 被页面 A 和 C 链接,A 的 PR 值略高于 B,页面 D 没有被任何页面链接(只有它链接出去),所以它的 PR 值最低,完全来自于 (1-d)/N 的部分。
优化与扩展
上面的实现是直观但效率较低的,尤其是在图很大的时候,内层循环 for (String pageT : graph.keySet()) 会导致大量的无效检查(检查 pageT 是否链接到 pageA)。
优化思路:使用反向链接
一个更高效的实现是预先计算一个反向链接图。
- 正向图:
graph.get(pageA)返回 A 链接到的页面列表。 - 反向图:
inLinksGraph.get(pageA)返回链接到 A 的页面列表。
有了反向图,计算 PR(A) 时,就不需要再遍历所有页面了,直接遍历 inLinksGraph.get(pageA) 即可。
优化后的代码片段
// 在 calculatePageRank 方法开始处
Map<String, List<String>> inLinksGraph = new HashMap<>();
for (String page : graph.keySet()) {
inLinksGraph.put(page, new ArrayList<>());
}
for (String fromPage : graph.keySet()) {
for (String toPage : graph.get(fromPage)) {
inLinksGraph.get(toPage).add(fromPage);
}
}
// ... 在迭代计算部分 ...
// 替换原来的内层循环
List<String> inLinksOfA = inLinksGraph.get(pageA);
if (inLinksOfA != null) {
for (String pageT : inLinksOfA) {
double prT = pageRanks.get(pageT);
int cT = outLinksCount.get(pageT);
prSum += prT / cT;
}
}
// ...
这个优化版本将时间复杂度从 O(N^2) 降低到了 O(E)(E 是边的数量),对于大规模网络图来说,性能提升非常显著,你可以尝试基于这个思路来重构代码。