double 类型本身没有固定的“小数位数”,它是一个二进制浮点数,而不是十进制浮点数,这意味着它无法精确表示所有十进制小数,这常常导致初学者困惑。
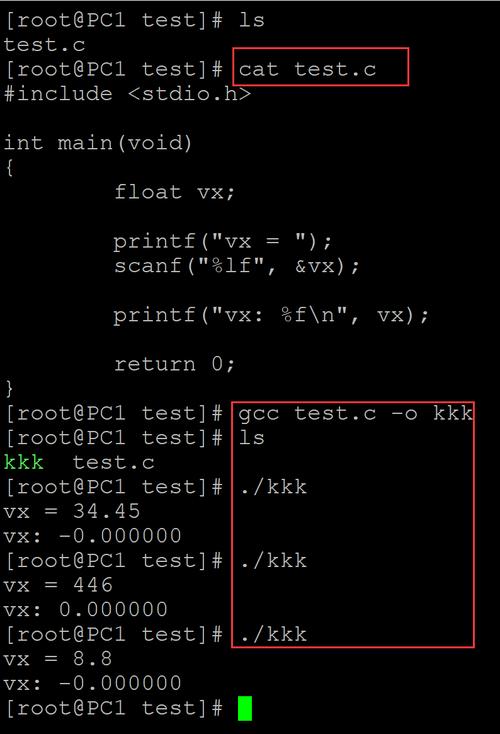
核心问题在于:计算机使用二进制(0和1),而人类习惯使用十进制(0-9)。
为什么 double 不精确?(根本原因)
double 在内存中存储的是一个二进制科学计数法形式的数字,由三部分组成:
- 符号位:正数或负数。
- 尾数:有效数字部分。
- 指数:决定小数点的位置。
关键点在于:只有某些特定的十进制小数才能被精确地转换为二进制。
经典例子:0.1
让我们看看十进制数 1 在 double 中是如何存储的。
public class DoublePrecision {
public static void main(String[] args) {
double d = 0.1;
System.out.println(d); // 输出 0.1,看起来没问题
System.out.println(d + 0.2); // 输出 0.30000000000000004,问题出现了!
}
}
为什么会这样?
十进制的 1 转换为二进制是一个无限循环小数:
1 (十进制) = 0.000110011001100110011... (二进制)
由于 double 的尾数位数是有限的(53位),计算机只能截取这个无限循环小数的一部分进行存储,它存储的并不是精确的 1,而是一个非常接近 1 的数,当你进行计算时,这个微小的误差会累积和放大,最终导致 1 + 0.2 的结果不是 3,而是 30000000000000004。
如何解决精度问题?(实践方案)
既然 double 天生不精确,那么在需要精确小数位数的场景(如金融计算)中,我们应该怎么办?
使用 BigDecimal 类(推荐)
java.math.BigDecimal 是专门为高精度计算设计的类,它以十进制的形式存储数字,因此可以完美地避免 double 的二进制精度问题。
使用 BigDecimal 的最佳实践:
import java.math.BigDecimal;
public class BigDecimalExample {
public static void main(String[] args) {
// 1. 使用 String 构造函数(最推荐的方式)
// 这可以避免直接使用 double 构造时引入的精度问题
BigDecimal bd1 = new BigDecimal("0.1");
BigDecimal bd2 = new BigDecimal("0.2");
// 2. 进行精确计算
BigDecimal sum = bd1.add(bd2);
// 3. 输出结果
System.out.println("使用 BigDecimal 计算 0.1 + 0.2 = " + sum); // 输出 0.3
// 4. 控制小数位数(四舍五入)
BigDecimal price = new BigDecimal("123.4567");
// 保留两位小数,使用 HALF_UP(四舍五入)模式
BigDecimal roundedPrice = price.setScale(2, RoundingMode.HALF_UP);
System.out.println("原价: " + price);
System.out.println("四舍五入到两位小数: " + roundedPrice); // 输出 123.46
}
}
BigDecimal 的核心要点:
- 用
String构造:new BigDecimal("0.1")是最安全的方式。 - 用
double构造有陷阱:new BigDecimal(0.1)会先将1这个不精确的double值传进去,结果仍然是不精确的。 - 使用
setScale()控制位数:这是设置最终显示或输出小数位数的主要方法。 - 指定舍入模式:如
RoundingMode.HALF_UP(四舍五入)、RoundingMode.DOWN(直接舍去)等。
使用 double + 格式化输出(仅用于显示)
如果你只是想 显示 时保留固定小数位数,但底层计算可以接受轻微误差,可以使用 String.format() 或 DecimalFormat。
重要提示:这 只是 格式化显示,并没有改变 double 变量本身的值,误差依然存在。
public class FormattingDouble {
public static void main(String[] args) {
double d = 3.1415926;
double imprecise = 0.1 + 0.2;
// 使用 String.format()
// %.2f 表示保留两位小数的浮点数
String formatted1 = String.format("保留两位小数: %.2f", d);
String formatted2 = String.format("0.1 + 0.2 显示为两位小数: %.2f", imprecise);
System.out.println(formatted1); // 输出 保留两位小数: 3.14
System.out.println(formatted2); // 输出 0.1 + 0.2 显示为两位小数: 0.30
System.out.println("------------------------------------");
// 使用 DecimalFormat
java.text.DecimalFormat df = new java.text.DecimalFormat("#.00");
String formatted3 = df.format(d);
String formatted4 = df.format(imprecise);
System.out.println(formatted3); // 输出 3.14
System.out.println(formatted4); // 输出 0.30
}
}
如何获取 double 的实际有效位数?
如果你想了解一个 double 变量在不丢失信息的情况下最多能有几位有效数字,可以使用 Double 类的静态方法。
public class GetPrecision {
public static void main(String[] args) {
double d1 = 123.456789;
double d2 = 1.23456789e10; // 12345678900.0
// Double.toString() 会返回一个能精确表示该 double 值的十进制字符串
String s1 = Double.toString(d1);
String s2 = Double.toString(d2);
// 计算字符串长度减去小数点
int precision1 = s1.length() - 1; // "123.456789" -> 9个字符,8位有效数字
int precision2 = s2.length() - 1; // "1.23456789E10" -> 11个字符,10位有效数字
System.out.println("d1 的有效数字位数: " + precision1);
System.out.println("d2 的有效数字位数: " + precision2);
// 更通用的方法
System.out.println("d1 的有效数字位数: " + getSignificantDigits(d1));
System.out.println("d2 的有效数字位数: " + getSignificantDigits(d2));
}
// 一个计算有效数字位数的辅助方法
public static int getSignificantDigits(double value) {
// 处理 0 和无穷大等特殊情况
if (value == 0.0 || Double.isInfinite(value) || Double.isNaN(value)) {
return 0;
}
// 使用科学计数法字符串,更容易计算
String s = String.format("%g", value);
// 移除符号和科学计数法部分 (如 'E10')
s = s.replaceAll("^[+-]?\\d+\\.?\\d*", "").replaceAll("[eE].*", "");
return s.length();
}
}
double 类型大约有 15-16位 十进制有效数字的精度,这意味着无论你的数字多大或多小,只要它能在 double 的表示范围内,它最多只有大约15位是准确的。
总结与对比
| 特性 | double |
BigDecimal |
|---|---|---|
| 数据类型 | 基本数据类型,二进制浮点数 | 引用类型,十进制浮点数 |
| 精度 | 约15-16位有效数字,不精确 | 可配置的任意精度,非常精确 |
| 性能 | 快,直接在CPU上运算 | 慢,基于软件实现,涉及对象创建 |
| 内存占用 | 固定(8字节) | 动态,取决于数字大小 |
| 适用场景 | 科学计算、图形学、游戏等对性能要求高且能接受微小误差的场景 | 金融、财务、电商等要求绝对精确计算的场景 |
| 如何控制小数位 | 仅通过 String.format() 或 DecimalFormat 格式化显示,不改变实际值 |
通过 setScale() 方法精确控制,并指定舍入模式 |
最终建议:
- 涉及钱、价格、数量等需要精确计算的,永远使用
BigDecimal。 - 用于非关键性的科学计算或显示,可以使用
double,但要注意其精度陷阱。 - 如果只是想把
double的结果显示成固定小数位,使用String.format()或DecimalFormat。