这是一个非常常见但又容易混淆的问题,核心要点是:double 本身不存储小数位数,它存储的是一个二进制的近似值。 我们通常看到的小数位数是格式化输出时控制的结果。

下面我们从几个方面来彻底搞懂这个问题。
核心问题:double 的精度是有限的
double 是一种浮点数类型,它遵循 IEEE 754 标准,用 二进制 来表示小数,就像我们熟悉的十进制无法精确表示 1/3 (0.333...) 一样,二进制也无法精确表示很多我们常见的十进制小数。
最经典的例子就是 1:
public class DoublePrecision {
public static void main(String[] args) {
double d = 0.1;
System.out.println(d); // 输出 0.1
// 看看它真实的二进制近似值
System.out.println(d + 0.2); // 输出 0.30000000000000004
}
}
为什么会这样?
因为 1 在二进制中是一个无限循环小数:0001100110011001100...。double 只有 64 位(1位符号位,11位指数位,52位尾数位)来存储它,所以只能截断,存储一个最接近的近似值,当你进行计算时,这个微小的误差会被放大,导致最终结果看起来“不精确”。
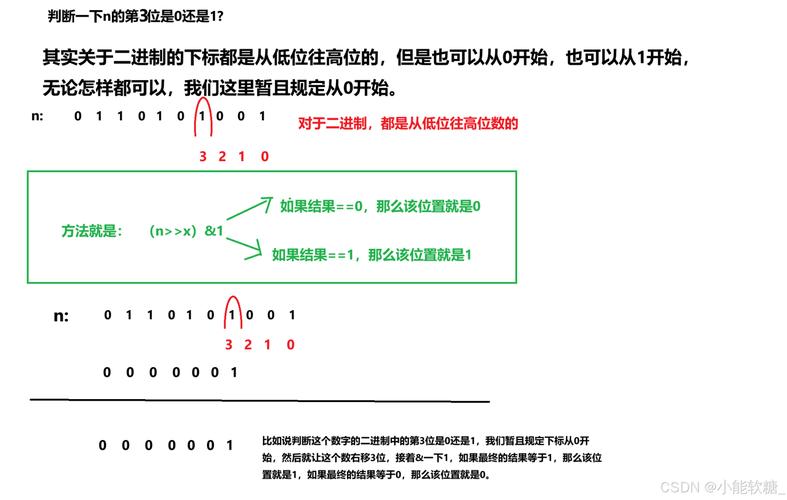
如何控制显示的小数位数?
既然 double 存储的是近似值,那么我们如何让它显示为我们想要的位数(比如两位小数)呢?答案是 格式化输出。
Java 提供了多种方式来格式化 double 的显示。
System.out.printf() (最常用)
使用 printf 和格式化字符串,类似于 C 语言。
double price = 123.456789;
// 保留两位小数,四舍五入
System.out.printf("价格: %.2f%n", price);
// 输出: 价格: 123.46
// 保留一位小数
System.out.printf("保留一位: %.1f%n", price);
// 输出: 保留一位: 123.5
// 不保留小数,四舍五入为整数
System.out.printf("整数: %.0f%n", price);
// 输出: 整数: 123
String.format()
如果你需要先格式化成字符串再使用,这个方法很方便。
double pi = 3.14159265;
String formattedPi = String.format("%.3f", pi);
System.out.println(formattedPi);
// 输出: 3.142
DecimalFormat (更灵活)
java.text.DecimalFormat 提供了更强大的格式化控制,比如添加千位分隔符。
import java.text.DecimalFormat;
double amount = 12345.6789;
DecimalFormat df1 = new DecimalFormat("#.##"); // # 表示数字,但不是必须的
System.out.println(df1.format(amount)); // 输出: 12345.68
DecimalFormat df2 = new DecimalFormat("0.00"); // 0 表示数字,如果不足会补0
System.out.println(df2.format(5.2)); // 输出: 5.20
DecimalFormat df3 = new DecimalFormat("#,###.00"); // 添加千位分隔符
System.out.println(df3.format(amount)); // 输出: 12,345.68
如何进行精确的十进制运算?
如果你在做的是金融、会计等对精度要求极高的场景,绝对不能直接使用 double,因为它的二进制近似值会累积误差,导致最终结果错误。
正确的做法是使用 java.math.BigDecimal 类。
BigDecimal 可以表示任意精度的十进制数,完美解决了 double 的精度问题。
import java.math.BigDecimal;
import java.math.RoundingMode;
public class BigDecimalExample {
public static void main(String[] args) {
// 使用 String 构造 BigDecimal,避免 double 的精度问题
BigDecimal bd1 = new BigDecimal("0.1");
BigDecimal bd2 = new BigDecimal("0.2");
// 加法
BigDecimal sum = bd1.add(bd2);
System.out.println("0.1 + 0.2 = " + sum); // 输出: 0.1 + 0.2 = 0.3
// 减法
BigDecimal difference = bd2.subtract(bd1);
System.out.println("0.2 - 0.1 = " + difference); // 输出: 0.2 - 0.1 = 0.1
// 乘法
BigDecimal product = bd1.multiply(bd2);
System.out.println("0.1 * 0.2 = " + product); // 输出: 0.1 * 0.2 = 0.02
// 除法 - 必须指定小数位数和舍入模式!
BigDecimal quotient = bd1.divide(bd2, 2, RoundingMode.HALF_UP);
System.out.println("0.1 / 0.2 = " + quotient); // 输出: 0.1 / 0.2 = 0.50
}
}
BigDecimal 的关键点:
- 用
String构造:永远不要用new BigDecimal(0.1)这种方式,因为它会把double的不精确值带进去,应该用new BigDecimal("0.1")。 - 除法必须指定舍入模式:
divide()方法在无法整除时,必须指定要保留的小数位数和舍入方式(如RoundingMode.HALF_UP是四舍五入),否则会抛出异常。
比较两个 double 是否相等
由于存在精度误差,永远不要使用 来比较两个 double 是否相等,应该判断它们的差值是否在一个非常小的“误差范围”内(这个范围称为 epsilon)。
public class DoubleComparison {
public static void main(String[] args) {
double a = 0.1 + 0.2;
double b = 0.3;
// 错误的方式!
System.out.println("a == b ? " + (a == b)); // 输出 false
// 正确的方式:定义一个误差范围
double epsilon = 0.000001;
boolean areEqual = Math.abs(a - b) < epsilon;
System.out.println("a 和 b 在误差范围内相等吗? " + areEqual); // 输出 true
}
}
总结与最佳实践
| 场景 | 推荐做法 | 原因 |
|---|---|---|
| 科学计算、图形学、游戏开发等对性能要求高,且能接受微小误差的场景。 | 使用 double |
运算速度快,遵循 IEEE 754 标准,是 CPU 硬件支持的。 |
| 金融、货币、会计等要求绝对精确十进制运算的场景。 | 使用 BigDecimal |
避免浮点数精度问题,保证计算的准确性。 |
| 需要控制显示的小数位数(保留两位小数显示给用户)。 | 使用 String.format() 或 DecimalFormat |
这只是格式化显示,不会改变 double 内部存储的近似值。 |
比较两个 double 是否相等 |
使用 Math.abs(a - b) < epsilon |
避免 因精度问题导致的错误判断。 |
记住一个黄金法则:
- 计算用
BigDecimal,显示用String.format。 - 如果只是做一些非精确要求的计算(比如游戏里的坐标、物理模拟),
double完全够用且高效,只要记住它是不精确的,并在显示时做好格式化即可。