冒泡排序是一种简单直观的排序算法,它之所以被称为“冒泡”,是因为在排序过程中,较大的元素会像水中的气泡一样,慢慢“浮”到数列的顶端(或者说,较小的元素会“沉”到数列的底端)。
算法原理
冒泡排序的核心思想是通过重复遍历要排序的数列,一次比较两个相邻的元素,如果它们的顺序错误(前一个比后一个大),就交换它们的位置。
这个过程会重复进行,直到整个数列有序。
具体步骤:
-
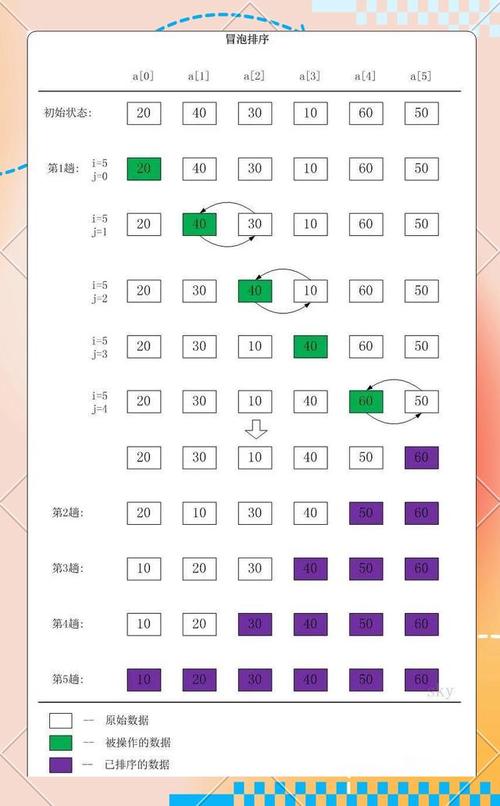
第一轮遍历:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 从第一个元素开始,比较它和第二个元素。
arr[0] > arr[1],则交换它们。 - 然后比较第二个元素和第三个元素。
arr[1] > arr[2],则交换它们。 - 以此类推,直到比较倒数第二个和最后一个元素。
- 完成第一轮后,数列中最大的元素会“冒泡”到最后一个位置。
- 从第一个元素开始,比较它和第二个元素。
-
第二轮遍历:
- 重复上述过程,但从第一个元素比较到倒数第二个元素(因为最后一个元素已经确定是最大的了)。
- 完成第二轮后,数列中第二大的元素会“冒泡”到倒数第二个位置。
-
后续轮次:
- 每一轮遍历,比较的范围都会减少一个(因为末尾的元素已经有序)。
- 这个过程持续进行,直到某一轮遍历中没有发生任何交换,说明数列已经完全有序,可以提前结束。
Python 代码实现
下面是冒泡排序的 Python 代码,包含了详细的注释来解释每一步。
基础实现
这个版本最直接地体现了算法的原理,但效率不是最高的。
def bubble_sort(arr):
"""
基础的冒泡排序实现
:param arr: 需要排序的列表
:return: 排序后的列表 (原地排序,也返回列表本身)
"""
n = len(arr)
# 外层循环控制排序的轮数
# 一共需要 n-1 轮
for i in range(n - 1):
# 内层循环控制每轮中比较的次数
# 每轮结束后,最大的元素会沉到最后,所以比较范围是 0 到 n-i-1
for j in range(0, n - i - 1):
# 如果前一个元素比后一个元素大,则交换它们
if arr[j] > arr[j + 1]:
# Python 中交换两个变量的值非常方便
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
# --- 示例 ---
my_list = [64, 34, 25, 12, 22, 11, 90]
print("原始列表:", my_list)
sorted_list = bubble_sort(my_list)
print("排序后列表:", sorted_list)
输出:
原始列表: [64, 34, 25, 12, 22, 11, 90]
排序后列表: [11, 12, 22, 25, 34, 64, 90]优化实现(加入提前终止)
如果某一轮遍历中没有任何元素发生交换,说明列表已经是有序的了,我们可以提前结束排序,这能大大提升在近乎有序的列表上的性能。
def optimized_bubble_sort(arr):
"""
优化后的冒泡排序实现,加入了提前终止的机制
:param arr: 需要排序的列表
:return: 排序后的列表
"""
n = len(arr)
# 外层循环控制排序的轮数
for i in range(n - 1):
# 标志位,用于记录本轮是否发生了交换
# 如果在一轮中没有发生交换,说明列表已经有序
swapped = False
# 内层循环
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# 如果发生了交换,将标志位置为 True
swapped = True
# 如果本轮没有发生交换,提前结束排序
if not swapped:
break
return arr
# --- 示例 ---
# 使用一个近乎有序的列表来测试优化效果
nearly_sorted_list = [2, 1, 3, 4, 5, 6, 7]
print("\n原始列表 (近乎有序):", nearly_sorted_list)
optimized_sorted_list = optimized_bubble_sort(nearly_sorted_list)
print("优化排序后列表:", optimized_sorted_list)
输出:
原始列表 (近乎有序): [2, 1, 3, 4, 5, 6, 7]
优化排序后列表: [1, 2, 3, 4, 5, 6, 7]在这个例子中,第一轮遍历会比较 2 和 1 并交换它们,然后后面的元素都是有序的,不会再发生交换,第二轮遍历时,swapped 变量会是 False,所以循环会直接 break,节省了不必要的遍历。
算法分析
-
时间复杂度:
- 最坏情况: O(n²),当输入列表是逆序时,每一轮都需要进行交换,总共需要进行大约
n(n-1)/2次比较和交换。 - 最好情况: O(n),当输入列表已经是有序时(优化后的版本),只需要进行一轮比较,没有发生交换,算法提前结束,比较次数为
n-1次。 - 平均情况: O(n²),对于随机顺序的列表,平均时间复杂度仍然是平方级别。
- 最坏情况: O(n²),当输入列表是逆序时,每一轮都需要进行交换,总共需要进行大约
-
空间复杂度:
- O(1),冒泡排序是原地排序算法,它不需要额外的存储空间来存储列表的副本,只使用了常数个额外变量(如
i,j,swapped)。
- O(1),冒泡排序是原地排序算法,它不需要额外的存储空间来存储列表的副本,只使用了常数个额外变量(如
-
稳定性:
- 稳定,在排序过程中,只有当
arr[j] > arr[j+1]时才会交换,这意味着相等的元素不会交换位置,它们原有的相对顺序会被保留下来。
- 稳定,在排序过程中,只有当
| 特性 | 描述 |
|---|---|
| 优点 | 实现简单,代码容易理解和编写。 空间复杂度低,是原地排序,不需要额外内存。 |
| 缺点 | 时间效率低,尤其是当数据量很大时,性能非常差。 |
| 适用场景 | 教学场景:作为学习排序算法的入门示例。 数据量极小:当需要排序的元素非常少时,其简单的实现可能比复杂算法更高效。 近乎有序的数据:优化后的版本在这种情况下表现尚可。 |
在实际的开发工作中,由于 Python 内置的 list.sort() 方法和 sorted() 函数(它们使用的是更高效的 Timsort 算法)已经非常成熟和快速,我们几乎不会手动实现冒泡排序来处理实际任务,理解冒泡排序的原理对于学习更复杂的排序算法(如快速排序、归并排序)打下坚实的基础。