核心问题:为什么 double 会丢精度?
根本原因在于 double 是一种浮点数类型,它用二进制(基于 2)来表示小数,而我们日常使用的是十进制(基于 10),这两种进制系统之间的转换,在很多时候是无法精确表示的。
浮点数的表示原理(IEEE 754 标准)
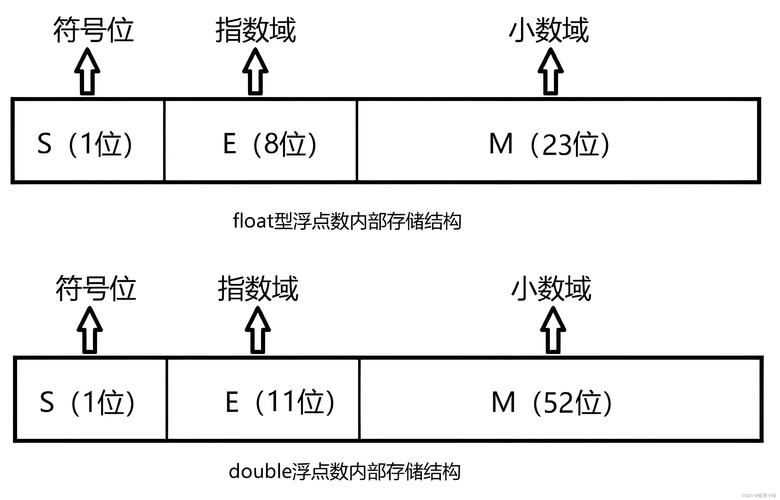
Java 的 double 遵循 IEEE 754 双精度浮点数标准,一个 double 值由三部分组成:
- 符号位:1 位,表示正负。
- 指数位:11 位,表示数值的放大或缩小倍数。
- 尾数位:52 位,表示数值的有效数字(精度部分)。
关键点:
double 能精确表示的数,必须满足它可以被表示为 尾数 * 2^指数 的形式,这就像十进制中,只有能表示为 尾数 * 10^指数 的数(如 0.5, 0.25, 0.125)才能被精确表示一样。
经典案例:十进制小数转二进制
我们来看一个最简单的例子:1
将十进制的 1 转换为二进制:
1 * 2 = 0.2-> 整数部分02 * 2 = 0.4-> 整数部分04 * 2 = 0.8-> 整数部分08 * 2 = 1.6-> 整数部分1(取走1,剩下0.6)6 * 2 = 1.2-> 整数部分1(取走1,剩下0.2)2 * 2 = 0.4-> 整数部分0(又回到了第2步)
你会发现,这个过程会无限循环下去:1 (十进制) = 00011001100110011... (二进制,无限循环)。
由于 double 的尾数位只有 52 位,它只能截取这个无限循环小数的前面一部分进行存储。计算机中存储的 1 并不是精确的 1,而是一个非常接近它的近似值。
验证代码
让我们用 Java 代码来验证这个现象:
public class DoublePrecision {
public static void main(String[] args) {
double d1 = 0.1;
double d2 = 0.2;
// 直接打印,JVM 会进行一些格式化,看起来可能没问题
System.out.println("d1: " + d1); // 输出: d1: 0.1
System.out.println("d2: " + d2); // 输出: d2: 0.2
// 使用 printf 格式化,可以看到更多小数位,真相暴露了
System.out.printf("d1 的真实值: %.20f%n", d1); // 输出: d1 的真实值: 0.10000000000000000555
System.out.printf("d2 的真实值: %.20f%n", d2); // 输出: d2 的真实值: 0.20000000000000001110
// 加法运算,误差被放大
double sum = d1 + d2;
System.out.println("0.1 + 0.2 = " + sum); // 输出: 0.1 + 0.2 = 0.30000000000000004
System.out.printf("0.1 + 0.2 的真实值: %.20f%n", sum); // 输出: 0.1 + 0.2 的真实值: 0.30000000000000004441
}
}
从代码中可以清晰地看到:

1在内存中实际存储的是10000000000000000555...2在内存中实际存储的是20000000000000001110...- 当这两个近似值相加时,结果自然不是
3,而是30000000000000004441...,这就是为什么1 + 0.2在代码中不等于3。
如何避免和解决精度问题?
根据应用场景的不同,有几种主流的解决方案。
使用 BigDecimal 类(金融计算首选)
java.math.BigDecimal 是专门为高精度计算设计的类,它可以表示任意精度的十进制数,避免了二进制和十进制转换的问题。
使用 BigDecimal 的注意事项:
-
使用
String构造函数:绝对不要使用double参数来构造BigDecimal,因为传入的double本身就是近似值,会把误差带进来。- 错误示范:
BigDecimal bd = new BigDecimal(0.1);// 内部还是会用不精确的 0.1 来构造 - 正确示范:
BigDecimal bd = new BigDecimal("0.1");// 直接从精确的字符串解析
- 错误示范:
-
使用
add,subtract,multiply,divide等方法进行运算:这些方法返回一个新的BigDecimal对象,而不是修改原对象。
示例代码:
import java.math.BigDecimal;
import java.math.RoundingMode;
public class BigDecimalExample {
public static void main(String[] args) {
// 正确构造 BigDecimal
BigDecimal bd1 = new BigDecimal("0.1");
BigDecimal bd2 = new BigDecimal("0.2");
// 加法
BigDecimal sum = bd1.add(bd2);
System.out.println("0.1 + 0.2 = " + sum); // 输出: 0.1 + 0.2 = 0.3
// 减法
BigDecimal difference = bd2.subtract(bd1);
System.out.println("0.2 - 0.1 = " + difference); // 输出: 0.2 - 0.1 = 0.1
// 乘法
BigDecimal product = bd1.multiply(bd2);
System.out.println("0.1 * 0.2 = " + product); // 输出: 0.1 * 0.2 = 0.02
// 除法 - 必须指定精度和舍入模式,否则会抛出异常
BigDecimal quotient = bd1.divide(bd2, 4, RoundingMode.HALF_UP); // 保留4位小数,四舍五入
System.out.println("0.1 / 0.2 = " + quotient); // 输出: 0.1 / 0.2 = 0.5000
}
}
使用 int 或 long(适用于“元/分”场景)
在金融系统中,如果所有金额都可以表示为“元”的整数倍(以“分”为单位),那么使用 int 或 long 是最简单、最高效、最精确的方式。
思路:将所有金额乘以 100,用整数进行存储和计算,最后需要显示时再除以 100。
示例代码:
public class IntegerMoneyExample {
public static void main(String[] args) {
// 以分为单位存储
int priceInCents = 100; // 1.00元
int discountInCents = 20; // 0.20元
// 直接进行整数运算,绝对精确
int finalPriceInCents = priceInCents - discountInCents; // 80分
// 转换为元,进行显示
double finalPriceInYuan = finalPriceInCents / 100.0;
System.out.println("最终价格: " + finalPriceInYuan + "元"); // 输出: 最终价格: 0.8元
}
}
优点:计算速度快,没有精度问题。 缺点:需要手动处理单位转换,代码可读性稍差,不适合小数位数不固定或非常多的场景。
使用 float(不推荐用于精度要求高的场景)
float 是单精度浮点数,精度比 double 更低(23位尾数),内存占用也更小(4字节 vs 8字节),除了在需要极致节省内存且对精度要求极低的场景(如某些图形学计算),几乎不推荐用于需要精确数值计算的场景,它同样存在 double 所有的精度问题。
总结与最佳实践
| 场景 | 推荐类型 | 原因 |
|---|---|---|
| 科学计算、一般工程计算 | double |
足够的精度和范围,性能较好,对微小误差不敏感。 |
| 金融、货币、会计等要求绝对精确的场景 | BigDecimal |
精确的十进制运算,避免二进制转换误差。 |
| 金融(以分为单位) | int / long |
性能最高,绝对精确,无误差。 |
| 需要极致节省内存且精度要求极低 | float |
精度低,不推荐用于一般计算。 |
核心要点回顾:
- 根本原因:
double是二进制浮点数,无法精确表示大部分十进制小数(如1,2)。 - 验证方法:使用
System.out.printf()打印足够多的小数位来观察真实值。 - 解决方案:
- 高精度计算:使用
BigDecimal,务必用String构造。 - 金融计算:优先考虑使用
int/long以“分”为单位。 float:除非有特殊需求,否则避免使用。
- 高精度计算:使用
- 代码中的“坑”:永远不要用
double来表示需要精确比较的值(如if (d == 0.1)),对于double的比较,应该判断它们的差值是否在一个极小的误差范围内(if (Math.abs(d - 0.1) < 1e-9))。