Java 解题核心思路
解题通常遵循以下四个步骤:

-
理解题意
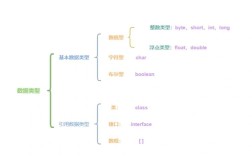
- 输入/输出: 明确函数的参数类型和返回值类型。
- 约束条件: 注意题目给出的数据范围(如数组长度、数值大小),这决定了你选择的算法的时间/空间复杂度是否可行。
- 边界条件: 思考特殊情况,如空数组、单个元素、所有元素相同等。
-
确定数据结构与算法
- 根据问题类型(数组、字符串、链表、树、图、动态规划等)选择合适的数据结构。
- 分析问题,找到最优的算法策略。
- 查找问题 -> 哈希表、二分查找
- 排序问题 -> 快速排序、归并排序
- 遍历问题 -> 深度优先搜索、广度优先搜索
- 最优问题 -> 动态规划、贪心算法
-
编写代码
- 将算法思路转化为清晰、规范的 Java 代码。
- 注意代码的健壮性,处理所有边界条件。
-
测试与优化
 (图片来源网络,侵删)
(图片来源网络,侵删)- 在 LeetCode 提交前,自己用几个测试用例(包括边界用例)跑一下。
- 提交后,根据结果(通过/超时/内存超限)进行优化。
Java 代码结构与通用模板
一个标准的 Java LeetCode 解题类通常如下结构:
import java.util.*; // 常常需要导入集合框架
public class Solution {
/**
* 主解题方法
* @param param1 参数1
* @param param2 参数2
* @return 返回值
*/
public int methodName(int[] param1, String param2) {
// 1. 处理边界条件
if (param1 == null || param1.length == 0) {
return 0; // 或其他默认值
}
// 2. 核心逻辑实现
// ...
// 3. 返回结果
return result;
}
// 如果需要,可以在此处定义辅助方法,如私有方法
private int helper(int x) {
return x * x;
}
// 对于一些类,如链表、二叉树,需要先定义节点类
// public class ListNode { ... }
// public class TreeNode { ... }
}
通用技巧:
- 使用
Arrays和Collections工具类:它们提供了很多便捷的排序、查找、转换等方法。 - 使用
StringBuilder:在频繁进行字符串拼接时,StringBuilder的性能远高于 号拼接。 - 善用
Map和Set:HashMap和HashSet是解决查找、去重、统计频率等问题的利器。
按题型分类的解题技巧与代码示例
数组 & 字符串
这是最基础的题型,核心是遍历、排序、查找和双指针。
- 技巧:
- 排序:
Arrays.sort()是 O(n log n) 的基础。 - 双指针:一个快指针,一个慢指针,常用于移除元素、寻找特定和等。
- 滑动窗口:用于处理子数组/子串问题,维护一个窗口来满足特定条件。
- 排序:
示例:移除元素 (LeetCode 27)

给你一个数组
nums和一个值val,你需要原地移除所有数值等于val的元素,并返回移除后数组的新长度。
class Solution {
public int removeElement(int[] nums, int val) {
// 使用双指针,slow 指向下一个不等于 val 的元素应该放置的位置
int slow = 0;
for (int fast = 0; fast < nums.length; fast++) {
// 如果当前元素不等于要移除的值
if (nums[fast] != val) {
// 将它放到 slow 的位置,slow 后移
nums[slow] = nums[fast];
slow++;
}
}
// slow 最终的值就是新数组的长度
return slow;
}
}
哈希表
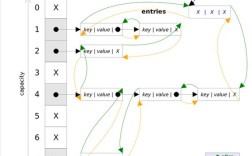
哈希表(HashMap, HashSet)是面试中的高频考点,核心是空间换时间。
- 技巧:
- 查找/去重:
HashSet可以在 O(1) 时间内完成。 - 频率统计:
HashMap<K, V>可以用来统计元素出现的次数。 - 查找补数:在求两数之和等问题中,可以用哈希表存储已遍历过的元素,快速查找目标值是否存在。
- 查找/去重:
示例:两数之和 (LeetCode 1)
给定一个整数数组
nums和一个整数目标值target,请你在该数组中找出和为目标值target的那两个整数,并返回它们的数组下标。
import java.util.Map;
import java.util.HashMap;
class Solution {
public int[] twoSum(int[] nums, int target) {
// key: 数值, value: 索引
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
// 检查补数是否已经存在于 map 中
if (map.containsKey(complement)) {
// 如果存在,返回当前索引和补数的索引
return new int[] { map.get(complement), i };
}
// 如果不存在,将当前元素和它的索引存入 map
map.put(nums[i], i);
}
// 题目保证有解,这里可以返回 null 或抛出异常
return null;
}
}
链表
链表操作的核心是指针的移动和指向。
- 技巧:
- 虚拟头节点:在处理头节点可能被删除的链表问题时,创建一个虚拟头节点可以简化逻辑。
- 快慢指针:一个指针每次走一步,一个指针每次走两步,常用于寻找环、寻找中间节点等。
- 递归:链表天然适合递归,但要注意递归深度和栈溢出问题。
示例:反转链表 (LeetCode 206)
反转一个单链表。
// Definition for singly-linked list.
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
class Solution {
// 方法一:迭代(双指针)
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while (curr != null) {
// 保存下一个节点
ListNode nextTemp = curr.next;
// 反转指针
curr.next = prev;
// prev 和 curr 后移
prev = curr;
curr = nextTemp;
}
// prev 最终指向新的头节点
return prev;
}
// 方法二:递归
public ListNode reverseListRecursive(ListNode head) {
// 递归终止条件
if (head == null || head.next == null) {
return head;
}
// 递归反转剩余部分
ListNode reversedList = reverseListRecursive(head.next);
// 将当前节点接到反转后链表的尾部
head.next.next = head;
head.next = null; // 防止形成环
return reversedList;
}
}
树
树(特别是二叉树)的遍历是基础,分为深度优先搜索和广度优先搜索。
- 技巧:
- DFS (前序、中序、后序):递归或栈实现。
- BFS (层序遍历):队列实现。
- 递归三要素:终止条件、递归调用、处理当前层。
示例:二叉树的前序遍历 (LeetCode 144)
给你二叉树的根节点
root,返回它前序遍历的结果。
// Definition for a binary tree node.
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
// 方法一:递归
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
helper(root, result);
return result;
}
private void helper(TreeNode node, List<Integer> result) {
if (node == null) {
return;
}
// 前序:根 -> 左 -> 右
result.add(node.val);
helper(node.left, result);
helper(node.right, result);
}
// 方法二:迭代(使用栈)
public List<Integer> preorderTraversalIterative(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
// 先压入右孩子,再压入左孩子,保证左孩子先出栈
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return result;
}
}
动态规划
DP 是难点,核心是找到状态转移方程。
- 技巧:
- 定义状态:
dp[i]或dp[i][j]代表什么。 - 找到状态转移方程:
dp[i]如何由dp[i-1],dp[i-2]等得到。 - 确定初始状态:
dp[0],dp[1]等的值。 - 考虑空间优化:有时可以将一维 DP 优化为常数空间。
- 定义状态:
示例:爬楼梯 (LeetCode 70)
假设你正在爬楼梯,需要
n阶你才能到达楼顶,每次你可以爬1或2个台阶,你有多少种不同的方法可以爬到楼顶?
class Solution {
public int climbStairs(int n) {
// dp[i] 表示爬到第 i 阶楼梯的方法数
// dp[i] = dp[i-1] + dp[i-2]
if (n == 1) {
return 1;
}
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
// 空间优化版本
public int climbStairsOptimized(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
int prev1 = 1; // dp[i-2]
int prev2 = 2; // dp[i-1]
int current = 0;
for (int i = 3; i <= n; i++) {
current = prev1 + prev2;
prev1 = prev2;
prev2 = current;
}
return current;
}
}
学习资源与社区
-
官方题解
LeetCode 每道题下方都有官方题解,通常是 C++ 版本,但思路清晰,是学习的首选。
-
优质社区题解
- LeetCode 评论区经常有非常精彩的 Java 解题思路,可以多看、多学习。
- 关注点赞数高的回答,通常代码质量高且思路清晰。
-
GitHub 仓库
- 搜索 "LeetCode Java" 可以找到很多开源的题解仓库,
gaurav5430/LeetCode,这些仓库整理了不同题目的解法,方便查阅。
- 搜索 "LeetCode Java" 可以找到很多开源的题解仓库,
-
博客与教程
- 算法可视化网站:VisuAlgo (https://visualgo.net) 可以帮助你直观地理解排序、搜索、树、图等算法。
- 技术博客:如 CSDN、掘金、知乎等,搜索具体题目名称,常有详细的图文解析。
刷题建议
- 循序渐进:从 "简单" 难度开始,建立信心,熟悉常见模式。
- 按专题刷:集中刷一个专题(如所有链表题、所有动态规划题),有助于归纳总结,形成知识体系。
- 多写多练:不要只看不写,亲手敲代码是检验是否掌握的唯一标准。
- 定期回顾:对于做错的题或经典题,要定期回顾,重新思考。
希望这份指南能对您有所帮助!祝您刷题顺利,早日成为算法大神!