判断二叉树是否为平衡二叉树
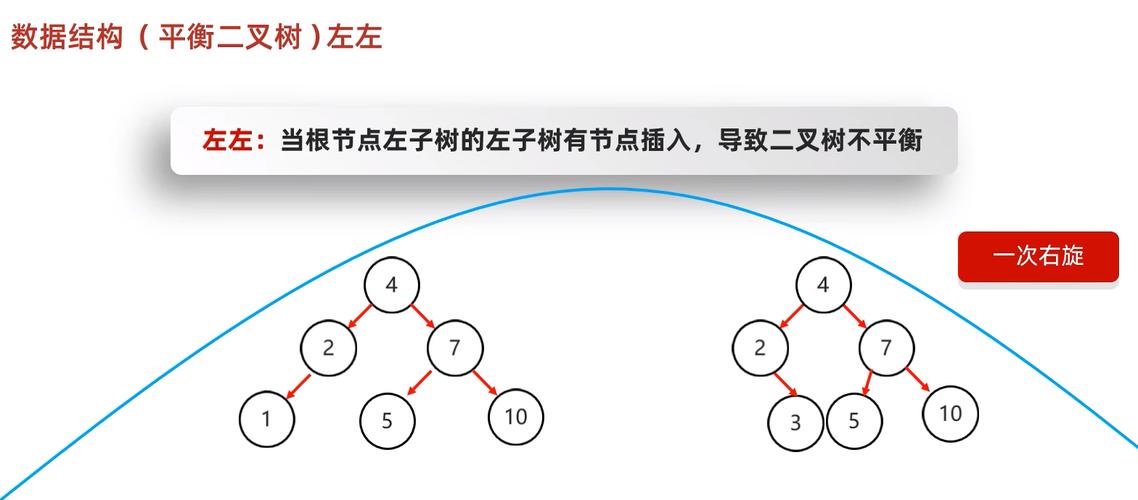
平衡二叉树(AVL树)是一种特殊的二叉搜索树,其中任何节点的两个子树的高度差不超过1,以下是判断二叉树是否为平衡二叉树的Java实现方法。

自顶向下递归
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
// 获取左右子树高度
int leftHeight = height(root.left);
int rightHeight = height(root.right);
// 检查当前节点是否平衡
if (Math.abs(leftHeight - rightHeight) > 1) {
return false;
}
// 递归检查左右子树
return isBalanced(root.left) && isBalanced(root.right);
}
// 辅助方法:计算树的高度
private int height(TreeNode node) {
if (node == null) return 0;
return Math.max(height(node.left), height(node.right)) + 1;
}
}
时间复杂度:O(n²),因为对于每个节点都要计算其高度,而计算高度的时间复杂度是O(n)。
自底向上递归(更高效)
class Solution {
public boolean isBalanced(TreeNode root) {
return checkHeight(root) != -1;
}
// 辅助方法:检查高度并返回-1表示不平衡
private int checkHeight(TreeNode node) {
if (node == null) return 0;
// 递归检查左子树
int leftHeight = checkHeight(node.left);
if (leftHeight == -1) return -1;
// 递归检查右子树
int rightHeight = checkHeight(node.right);
if (rightHeight == -1) return -1;
// 检查当前节点是否平衡
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
// 返回当前节点的高度
return Math.max(leftHeight, rightHeight) + 1;
}
}
时间复杂度:O(n),因为每个节点只被访问一次。
使用类变量存储结果
class Solution {
private boolean balanced = true;
public boolean isBalanced(TreeNode root) {
height(root);
return balanced;
}
private int height(TreeNode node) {
if (node == null || !balanced) return 0;
int leftHeight = height(node.left);
int rightHeight = height(node.right);
if (Math.abs(leftHeight - rightHeight) > 1) {
balanced = false;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
这种方法与方法二类似,但使用类变量来存储平衡状态。
测试示例
public class Main {
public static void main(String[] args) {
// 构建平衡二叉树
TreeNode balancedTree = new TreeNode(1);
balancedTree.left = new TreeNode(2);
balancedTree.right = new TreeNode(3);
balancedTree.left.left = new TreeNode(4);
balancedTree.left.right = new TreeNode(5);
// 构建非平衡二叉树
TreeNode unbalancedTree = new TreeNode(1);
unbalancedTree.left = new TreeNode(2);
unbalancedTree.left.left = new TreeNode(3);
unbalancedTree.left.left.left = new TreeNode(4);
Solution solution = new Solution();
System.out.println("Balanced tree is balanced: " +
solution.isBalanced(balancedTree)); // true
System.out.println("Unbalanced tree is balanced: " +
solution.isBalanced(unbalancedTree)); // false
}
}
推荐使用方法二(自底向上递归),因为它的时间复杂度最优(O(n)),空间复杂度为O(n)(最坏情况下为树的高度),这种方法通过一次遍历即可完成判断,避免了重复计算高度。