Java数据结构与算法，如何高效实现与优化？-杰瑞科技汇

引言：为什么学习数据结构与算法？
基础概念
- 数据结构
- 算法
- 复杂度分析
线性数据结构
- 数组
- 链表
- 栈
- 队列
非线性数据结构
- 树
  - 二叉树
  - 二叉搜索树
  - 堆
  - 平衡树 (AVL树, 红黑树 - 简述)
- 哈希表
- 图
核心算法
- 排序算法
- 搜索算法
- 递归与分治
- 动态规划
- 贪心算法
总结与学习建议

引言：为什么学习数据结构与算法？

数据结构与算法是计算机科学的基石，它们决定了程序运行效率和资源消耗。

（图片来源网络，侵删）

好的数据结构 + 好的算法 = 高效的程序：在用户列表中查找一个用户，使用数组需要遍历（O(n)），而使用哈希表可能只需要O(1)时间。
面试的敲门砖：几乎所有知名的科技公司都将数据结构与算法作为面试的核心考察内容。
解决复杂问题的能力：掌握它们能让你更清晰地思考问题，设计出更优雅、更健壮的解决方案。

基础概念

数据结构

数据结构是计算机中存储、组织数据的方式，它不仅要存储数据,还要支持高效地访问和修改数据。

分类：
- 线性结构：数据元素之间存在一对一的线性关系，如：数组、链表、栈、队列。
- 非线性结构：数据元素之间存在一对多或多对多的关系，如：树、图、哈希表。

算法

算法是解决特定问题步骤的有限序列,它具有以下特性：

输入：有零个或多个输入。
输出：至少有一个输出。
有穷性：算法必须在执行有限步骤后终止。
确定性：每一步都有确切的含义,无歧义。
可行性：每一步都是可行的。

复杂度分析

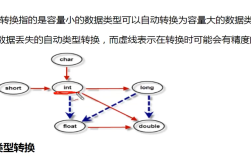
衡量算法好坏的核心指标，通常使用大O表示法来描述。

时间复杂度：估算算法执行时间与数据规模n的增长关系。
- O(1) - 常数时间 (最优)
- O(log n) - 对数时间 (优秀,如二分查找)
- O(n) - 线性时间 (良好,如遍历数组)
- O(n log n) - 线性对数时间 (很好,如高效排序算法)
- O(n²) - 平方时间 (一般,如简单排序算法)
- O(2ⁿ) - 指数时间 (很差,如暴力解决旅行商问题)
空间复杂度：估算算法执行所需额外存储空间与数据规模n的增长关系。

线性数据结构

数组

描述：在内存中连续存储的元素集合,通过索引访问。
（图片来源网络，侵删）
特点：
- 优点：通过索引访问元素非常快（O(1)）。
- 缺点：大小固定，插入和删除元素需要移动大量元素（O(n)）。
Java实现：java.util.ArrayList 是动态数组的实现,可以自动扩容。

示例代码：

import java.util.ArrayList;
public class ArrayExample {
    public static void main(String[] args) {
        // 创建一个动态数组
        ArrayList<String> fruits = new ArrayList<>();
        // 添加元素
        fruits.add("Apple");
        fruits.add("Banana");
        fruits.add("Cherry");
        // 通过索引访问
        System.out.println("First fruit: " + fruits.get(0)); // O(1)
        // 遍历
        for (String fruit : fruits) {
            System.out.println(fruit);
        }
        // 在中间插入 (效率低)
        fruits.add(1, "Blueberry"); // O(n)
        // 删除元素 (效率低)
        fruits.remove("Banana"); // O(n)
    }
}

链表

描述：由一系列节点组成,每个节点包含数据和指向下一个节点的指针。
特点：
- 优点：大小不固定，插入和删除元素非常快（O(1)，如果已知节点位置）。
- 缺点：访问元素需要从头遍历（O(n)），内存开销较大（每个节点都需要存储指针）。
Java实现：java.util.LinkedList。

示例代码：

import java.util.LinkedList;
public class LinkedListExample {
    public static void main(String[] args) {
        LinkedList<String> names = new LinkedList<>();
        names.add("Alice");
        names.add("Bob");
        names.addFirst("Zoe"); // O(1)
        names.addLast("Charlie"); // O(1)
        System.out.println("First name: " + names.getFirst()); // O(1)
        System.out.println("Last name: " + names.getLast()); // O(1)
        names.remove("Bob"); // O(n) 需要先找到
        for (String name : names) {
            System.out.println(name);
        }
    }
}

栈

描述：一种后进先出的数据结构,像一摞盘子。
操作：push (入栈), pop (出栈), peek (查看栈顶)。
Java实现：java.util.Stack (不推荐，因为它是线程安全的但性能稍差) 或 java.util.LinkedList 来模拟栈操作。
应用：函数调用栈、表达式求值、括号匹配。

示例代码：

import java.util.Stack;
public class StackExample {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();
        stack.push(10);
        stack.push(20);
        stack.push(30);
        System.out.println("Top of stack: " + stack.peek()); // 30
        int poppedValue = stack.pop();
        System.out.println("Popped value: " + poppedValue); // 30
        System.out.println("Is stack empty? " + stack.isEmpty());
    }
}

队列

描述：一种先进先出的数据结构,像排队买票。
操作：enqueue (入队), dequeue (出队)。
Java实现：java.util.Queue 是接口，常用实现类有 LinkedList 和 ArrayDeque。
应用：任务调度、广度优先搜索。

示例代码：

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
    public static void main(String[] args) {
        Queue<String> queue = new LinkedList<>();
        queue.add("Customer 1");
        queue.add("Customer 2");
        queue.add("Customer 3");
        System.out.println("Head of queue: " + queue.peek()); // Customer 1
        String servedCustomer = queue.poll(); // O(1)
        System.out.println("Served customer: " + servedCustomer); // Customer 1
        System.out.println("Queue size: " + queue.size());
    }
}

非线性数据结构

树

描述：一种分层的数据结构，由节点和边组成，有一个根节点,且没有环路。
二叉树：每个节点最多有两个子节点（左、右）。
二叉搜索树：一种特殊的二叉树，左子树所有节点值 < 根节点值 < 右子树所有节点值，查找、插入、删除的平均时间复杂度为 O(log n)。
堆：一种特殊的完全二叉树。
- 最大堆：父节点的值总是大于或等于其子节点的值。
- 最小堆：父节点的值总是小于或等于其子节点的值。
- Java实现：java.util.PriorityQueue 默认是最小堆。

示例代码 (BST 和 PriorityQueue)：

// 1. 手动实现一个简单的二叉搜索树节点
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int val) { this.val = val; }
}
// 2. 使用 Java 的 PriorityQueue (最小堆)
import java.util.PriorityQueue;
public class TreeExample {
    public static void main(String[] args) {
        // PriorityQueue 示例
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        minHeap.add(10);
        minHeap.add(5);
        minHeap.add(20);
        minHeap.add(1);
        // 出队顺序将是升序
        System.out.println("Polling from min-heap:");
        while (!minHeap.isEmpty()) {
            System.out.println(minHeap.poll()); // 1, 5, 10, 20
        }
    }
}

哈希表

描述：通过哈希函数将键映射到存储桶（数组索引）以实现快速访问的数据结构。
特点：理想情况下，插入、删除、查找的平均时间复杂度为 O(1)。
冲突：两个不同的键可能映射到同一个索引，Java的HashMap使用链地址法（拉链法）和红黑树来解决冲突。
Java实现：java.util.HashMap, java.util.HashSet。

示例代码：

import java.util.HashMap;
import java.util.Map;
public class HashMapExample {
    public static void main(String[] args) {
        Map<String, Integer> studentGrades = new HashMap<>();
        // 插入
        studentGrades.put("Alice", 95);
        studentGrades.put("Bob", 88);
        // 查找
        System.out.println("Alice's grade: " + studentGrades.get("Alice")); // O(1)
        // 检查是否存在
        System.out.println("Contains Bob? " + studentGrades.containsKey("Bob"));
        // 遍历
        for (Map.Entry<String, Integer> entry : studentGrades.entrySet()) {
            System.out.println("Student: " + entry.getKey() + ", Grade: " + entry.getValue());
        }
    }
}

图

描述：由顶点和边组成,用于表示多对多的关系。
存储方式：
- 邻接矩阵：二维数组，matrix[i][j] = 1 表示顶点 i 和 j 之间有边,适合稠密图。
- 邻接表：数组 + 链表/动态数组，graph[i] 存储与顶点 i 相邻的所有顶点,适合稀疏图。
Java实现：没有内置的图类，通常使用 HashMap<Integer, List<Integer>> 或自定义类来实现邻接表。
应用：社交网络、地图导航、推荐系统。

示例代码 (邻接表表示)：

import java.util.*;
public class GraphExample {
    private Map<Integer, List<Integer>> adjList;
    public GraphExample() {
        this.adjList = new HashMap<>();
    }
    public void addVertex(int vertex) {
        adjList.putIfAbsent(vertex, new ArrayList<>());
    }
    public void addEdge(int v1, int v2) {
        addVertex(v1);
        addVertex(v2);
        adjList.get(v1).add(v2);
        adjList.get(v2).add(v1); // 无向图
    }
    public static void main(String[] args) {
        GraphExample graph = new GraphExample();
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 3);
        System.out.println("Adjacency List:");
        System.out.println(graph.adjList);
        // 输出: {0=[1, 2], 1=[0, 2], 2=[0, 1, 3], 3=[2]}
    }
}

核心算法

排序算法

算法	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性	Java实现
冒泡排序	O(n²)	O(n²)	O(1)	稳定	-
选择排序	O(n²)	O(n²)	O(1)	不稳定	-
插入排序	O(n²)	O(n²)	O(1)	稳定	-
归并排序	O(n log n)	O(n log n)	O(n)	稳定	`Arrays.sort()` (对象)
快速排序	O(n log n)	O(n²)	O(log n)	不稳定	`Arrays.sort()` (基本类型)
堆排序	O(n log n)	O(n log n)	O(1)	不稳定	-

示例代码 (快速排序)：

public class QuickSort {
    public static void sort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);
            sort(arr, low, pi - 1);
            sort(arr, pi + 1, high);
        }
    }
    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = (low - 1);
        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;
                swap(arr, i, j);
            }
        }
        swap(arr, i + 1, high);
        return i + 1;
    }
    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    public static void main(String[] args) {
        int[] data = {8, 7, 2, 1, 0, 9, 6};
        System.out.println("Unsorted Array: " + Arrays.toString(data));
        sort(data, 0, data.length - 1);
        System.out.println("Sorted Array: " + Arrays.toString(data));
    }
}

搜索算法

线性搜索：遍历整个数组，O(n)。
二分搜索：在有序数组中进行，每次将搜索范围减半，O(log n)。

示例代码 (二分搜索)：

public class BinarySearch {
    public static int search(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] == target) {
                return mid;
            } else if (arr[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1; // 未找到
    }
    public static void main(String[] args) {
        int[] sortedArray = {1, 3, 5, 7, 9, 11, 13};
        int target = 7;
        int result = search(sortedArray, target);
        if (result == -1) {
            System.out.println("Element not found.");
        } else {
            System.out.println("Element found at index: " + result);
        }
    }
}

递归与分治

递归：一个函数在其内部调用自身。
- 关键：基本情况 和 递归情况。
- 示例：计算阶乘、斐波那契数列、树的遍历。
分治：将一个大问题分解成若干个相同或相似的子问题，递归解决子问题，最后将子问题的解合并。
- 示例：归并排序、快速排序。

动态规划

思想：通过存储子问题的解来避免重复计算，从而解决复杂问题,通常用于优化问题。
核心：状态定义 和 状态转移方程。
适用条件：最优子结构、重叠子问题。
示例：斐波那契数列（优化版）、背包问题、最长公共子序列。

贪心算法

思想：在每一步选择中都采取当前状态下看起来最优的选择,从而希望导致结果是全局最优的。
特点：简单、高效，但不一定能得到全局最优解。
示例：找零钱问题（特定面额）、Dijkstra最短路径算法、Prim最小生成树算法。

总结与学习建议

理论与实践结合：不要只看书或看视频，一定要亲手敲代码实现每个数据结构和算法，从最基础的开始，如链表、二叉树、排序算法。
理解优于记忆：理解每个数据结构的设计思想和每个算法的核心逻辑，比死记硬背代码重要得多，问自己“为什么这样设计？”和“它解决了什么问题？”。
画图辅助：对于链表、树、图等结构，画图是理解其操作（如插入、删除、遍历）的最好方式。
学习Java集合框架：深入研究 java.util 包下的核心类，如 ArrayList, LinkedList, HashMap, HashSet, TreeMap, PriorityQueue，阅读它们的源码，了解它们是如何实现对应数据结构的，以及它们做了哪些优化（如 HashMap 的扩容机制和红黑树转换）。
刷题：在 LeetCode、HackerRank 等平台上刷题是检验和提升能力的最佳途径，从 "简单" 难度的题开始，逐步挑战 "中等" 和 "困难" 的题。
分析复杂度：写完代码后,养成分析其时间和空间复杂度的习惯。

学习数据结构与算法是一个漫长但回报丰厚的过程，坚持下去,你的编程能力和解决问题的能力将会有质的飞跃。

Java数据结构与算法，如何高效实现与优化？

目录

引言：为什么学习数据结构与算法？

基础概念

数据结构

算法

复杂度分析

线性数据结构

数组

链表

栈

队列

非线性数据结构

树

哈希表

图

核心算法

排序算法

搜索算法

递归与分治

动态规划

贪心算法

总结与学习建议

99ANYc3cd6

Java HTTP与Socket有何本质区别？

Python filehandler如何高效操作文件？

苹果电脑怎么装Win7？

Python中periodogram如何实现频谱分析？

Python tkconstants是什么？如何使用？

男士瑜伽入门，哪些基本动作必学？

Redis视频教程如何结合Java开发实战？

Python数组如何实现连接操作？

Python如何下载图片？

Java中GBK与UTF-8编码如何转换？

mac 10.10如何安装？步骤有哪些？

SecureCRT Python脚本如何实现自动化操作？

PowerPoint教程PPT，如何快速制作专业幻灯片？

Python3.6如何兼容TensorFlow？

Android如何运行Java程序？

Java应用与Web开发有何关联？

Java数据结构与算法，如何高效实现与优化？

目录

引言：为什么学习数据结构与算法？

基础概念

数据结构

算法

复杂度分析

线性数据结构

数组

链表

栈

队列

非线性数据结构

树

哈希表

图

核心算法

排序算法

搜索算法

递归与分治

动态规划

贪心算法

总结与学习建议

相关推荐

男士瑜伽入门，哪些基本动作必学？